Root Mean Square Error

 




What is rmse? :-The error of a model in predicting quantitative data is often measured using the Root Mean Square Error (RMSE).


Let's try to investigate the mathematical justification for this measure of inaccuracy. The first thing we can see is a similarity to the formula for the Euclidean distance between two vectors in Rn, ignoring the division by n beneath the square root:

Heuristically, this suggests that RMSE may be seen as a distance between the vector of expected values and the vector of observed values.

But why are we doing this division by n here under the square root? The Euclidean distance is only scaled down by a factor of (1/n) if we maintain n (the number of observations) constant. It's a little difficult to see why this is the appropriate course of action, so let's go a little more.

Imagine that the following happens when we add random "errors" to each of the predicted values to create our observed values:



Considered random variables, these mistakes may have a Gaussian distribution with mean and standard deviation, but any other distribution with a square-integrable PDF (probability density function) would also work. We want to think of I as a fundamental physical number, such as the precise separation between Mars and the Sun at a specific moment. Our observed number Yi would therefore represent the measured distance between Mars and the Sun, with some mistakes resulting from telescope calibration issues and measurement noise caused by air interference.

The mean of our error distribution would represent a lingering bias resulting from calibration mistake, and the standard deviation would represent the amount of measurement noise. Imagine that we now have a precise understanding of the mean of the distribution of our mistakes and would like to project the standard deviation. With a little math, we can determine that:

Notice how familiar the left side appears to be! It is exactly our RMSE calculation from previously if we remove the expectation E[...] from within the square root. According to the central limit theorem, the variance of the variable I (i — yi)2 / n = I (i)2 / n should converge to zero as n increases. In fact, a sharper version of the central limit theorem states that its variance should asymptotically approach zero like 1/n. This demonstrates that I (i — yi)2 / n is a reliable estimate for E[i (i — yi)2 / n] = 2. However, RMSE is a reliable estimate of the standard deviation of our error distribution. rs!

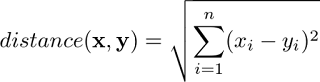
Comments

Post a Comment

Popular posts from this blog

Tanh Activation Function

Image
With a difference in output range of -1 to 1, the tanh activation function is remarkably similar to the sigmoid/logistic activation function, and even has the same S-shape. The larger the input (more positive), the closer the output to 1.0, and the smaller the input (more negative), the closer the output to -1.0. Mathematically it can be represented as: The following are some of the benefits of using this activation function: We can simply map the output values as strongly negative, neutral, or very positive because the tanh activation function's output is Zero centred. Because its values range from -1 to, it's commonly utilised in hidden layers of neural networks. As a result, the hidden layer's mean is 0 or extremely close to it. It aids in data centering and makes learning the next layer much simpler. To understand the tanh activation function's limits, look at its gradient. As you can see, it, like the sigmoid activation function, has the problem of vanishing gradi
Read more

Sigmoid Activation Function And Its Uses.

Image
The sigmoid activation function is a mathematical function commonly used in artificial neural networks and machine learning models. It maps the input values to a range between 0 and 1, providing smooth and continuous output. The sigmoid function is defined as: σ(x) = 1 / (1 + e^(-x)) Where: x is the input to the function e is the base of the natural logarithm (approximately 2.71828) The sigmoid function has an S-shaped curve that increases from 0 to 1 as the input value increases. It has the desirable property of being differentiable, which is a valuable for training neural networks using gradient-based optimization algorithms like backpropagation. One of the main applications of the sigmoid function is in binary classification problems, where the goal is to assign inputs to one of two classes. The sigmoid function is commonly used as the activation function in the output layer of a neural network for this purpose. The output value, between 0 and 1, can be interpreted as the pro
Read more

Unleashing Creativity: The Latest Frontier of Animation AI

Image
 Introduction Animation AI is the result of the convergence of technology and creativity in the animation field. This groundbreaking fusion has not only transformed the animation landscape but also opened up exciting avenues for artists, storytellers, and tech enthusiasts alike. In this blog, we delve into the latest trends, advancements, and possibilities that Animation AI brings to the table. Lifelike Character Animation AI-driven character animation has taken realism to unprecedented levels. With machine learning algorithms studying human motion, characters move and interact in ways that mirror real-life actions. Expressions and emotions are portrayed authentically, immersing audiences in narratives that tug at heartstrings. Efficiency and Speed Automation is a hallmark of Animation AI. Inbetweening, traditionally a meticulous manual process, is now accelerated by AI, reducing production time. Creative minds can focus on refining the narrative while AI handles the technical intr
Read more